
Cuncursos, Vestibulares, Vestibulinhos e Carreira Militar
Links Patrocinados
Concursos
Vestibulares
Vestibulinhos
Carreira Militar
Material de Estudo
Links Patrocinados
Publicidade
Links Patrocinados
Inequações
do 2o grau
Para
resolvermos uma inequação do 2o grau, utilizamos o estudo do sinal.
As inequações são representadas pelas desigualdades: > , >
, < , < .
Ex:
I) x2 – 3x +6 > 0
Resolução:
x2 – 3x +6 = 0
x´= 1, x´´ = 2
Como desejamos os valores para os quais a função é maior
que zero devemos fazer um esboço do gráfico e ver para quais valores
de x isso ocorre.
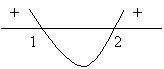
Vemos,
que as regiões que tornam positivas a função são: x<1 e x>2
Resposta: {xÎR| x<1 ou x>2}
Inequações simultâneas
Ex:
-8 < x2 –2x –8 < 0
Resolução:
1o passo) Separar as inequações , obedecendo o intervalo
dado.
Temos: I) x2 – 2x –8 > -8 e II) x2 –2x –8 <0
2o passo) Determinar as raízes ou zeros de cada uma
das funções obtidas pela separação.
I) x2 – 2x > 0 II) x2 –2x –8 <0x´ = 0 x´= x´´ = 1x´´ = 2
I)x<0 ou x>2 II)x
diferente de 1.
II)x
diferente de 1.
4o passo) Calcular a solução S, que é dada pela interseção
dos intervalos de S1 e S2.
Obs: o quadro
de resposta será preenchido pelo intervalo achado.
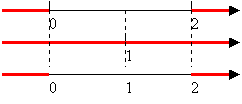
Resposta: {xÎR| x<0 ou x>2}
o
Inequação produto e inequação quociente,
São
as desigualdades da forma: f(x) . g(x) > 0, f(x) . g(x) < 0, f(x)
.g(x) > 0 e f(x) .g(x) < 0. f(x) / g(x) > 0, f(x) / g(x) < 0, f(x) / g(x) >
0 e f(x) / g(x) < 0, respectivamente.
Ex:
I) (x2 –9x –10) (x2 – 4x +4) < 0
Resolução:
1o passo) Trabalhar f(x) e g(x) separadamente
x2 –9x –10 = 0 (I)x2 – 4x +4 = 0 (II)
2o passo) Determinar as raízes das funções
(I)
x´= -1, x´´ = 10
(II)
x´= x´´ = 2
3o passo) Fazer o estudo do sinal para cada função.

I) x<-1 ou x>10
II) x¹2
4o passo) Calcular a solução, que é dado pelo sinal
de desigualdade da função de origem, isto é:
> intervalo
positivo e bolinha fechada
> intervalo positivo e bolinha aberta
< intervalo negativo e bolinha fechada
< intervalo negativo e bolinha aberta
Obs1: no quadro de respostas (ou soluções), se os intervalos
forem em: f(x) positivo e g(x)positivo o h(x) será +, assim temos: +
e + = + ; + e - = - ; - e + = - ; - e - = +
Obs2: Na inequação quociente observar a CE do denominador,
que influenciará o resultado nos intervalos, no que diz respeito a intervalo
fechado ou aberto
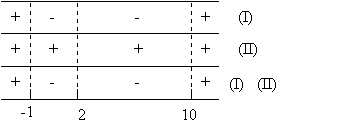
Assim, as únicas regiões positivas (maiores que zero)
são em x<-1 e x>10
Resposta: {xÎR| x<-1 ou x>10}